ACTIVIDAD 1. ORDEN EN LAS OPERACIONES
A. Explicación
En tu cuaderno escribe la siguiente información.
El orden correcto a la
hora de resolver operaciones es importante. Es necesario resolver cada parte de
la operación en el orden adecuado. Este orden o jerarquía a la hora de resolver
operaciones combinadas es el siguiente:
- Paréntesis
- Multiplicaciones y divisiones
- Sumas y restas
Lo primero que se debe
resolver es aquello que esté dentro de un paréntesis. En caso de que la operación
combinada no incluya paréntesis, hay que pasar a lo siguiente en la
jerarquía. Después de resolver los paréntesis (o saltarlos si no lo lleva), lo
siguiente que debemos hacer es resolver las multiplicaciones (conocer las tablas de multiplicar ayuda)
y divisiones, en orden de izquierda a derecha.
Por último, después de los paréntesis, multiplicaciones y divisiones, lo siguiente serán las sumas y restas. Estas se resolverán en orden, de izquierda a derecha.
B. Afianzamiento
Escribe en tu cuaderno
los siguientes ejemplos.
Vamos a resolver una
operación con paréntesis, multiplicaciones, divisiones, sumas
y restas.
2+(8×3-6)+4×5-(28:2):2+16=
1. Paréntesis
Primero resolvemos los
paréntesis. En caso de haber operaciones diferentes dentro del paréntesis,
resolveremos en el siguiente orden: primero multiplicaciones y divisiones,
después sumas y restas:
2+(8×3-6)+4×5-(28:2):2+16=
2+(24-6)+4×5-14:2+16=
2+18+4×5-14:2+16=
2. Multiplicaciones
y divisiones
Una vez eliminados los
paréntesis, lo siguiente que vamos a resolver son las multiplicaciones y las
divisiones. En este caso, se resuelven en orden, de izquierda a derecha.
2+18+4×5-14:2+16=
2+18+20-7+16=
3. Sumas y restas
Para terminar, lo
último que resolvemos son las sumas y restas. Al igual que en el punto
anterior, las resolveremos de izquierda a derecha.
2+18+20-7+16=49
El resultado de la
operación sería:
2+(8×3-6)+4×5-(28:2):2+16=
49
C. Ejercitación
Resuelve en tu cuaderno las siguientes
operaciones
2.1. EXPLORACIÓN: Escribe en tu cuaderno la siguiente información
2.2.
AFIANZAMIENTO: Resuelve las siguientes actividades en tu cuaderno
de matemáticas
2.3. EJERCITACIÓN: Resuelve las siguientes actividades en tu cuaderno y envía fotos al WhatsApp como evidencia de tu trabajo.

ACTIVIDAD 3. POTENCIACIÓN
3.1. EXPLICACIÓN
Para ir
introduciendo el tema, mira con atención el siguiente video.
En tu
cuaderno escribe la siguiente información
La potenciación
Las potencias son una manera abreviada de
escribir una multiplicación formada por varios números iguales. Son muy útiles para
simplificar multiplicaciones donde se repite el mismo número.
Las potencias están
formadas por la base y por el exponente. La base es el número que se
está multiplicando varias veces y el exponente es el número de veces que se
multiplica la base.
¿Qué es la base? Es el número que se está multiplicando.
· ¿Qué número se está
multiplicando? El 5, por lo tanto es la BASE
· ¿Cuántas veces se
repite el número? 7 veces, por lo tanto, es el EXPONENTE
Escribiendo la potencia quedaría así:
· ¿Qué número se está
multiplicando? El 3, por lo tanto, es la BASE
· ¿Cuántas veces se repite el número? El número se repite 4 veces, por lo tanto, es el EXPONENTE
3 x 3 x 3 x 3 = 3 4
3.2. AFIANZAMIENTO: Resuelve las siguientes potencias para ir practicando.
3.3. EJERCITACIÓN: Resuelve las páginas 64, 65, 66 y 67 de tu libro de trabajo
ACTIVIDAD 4. RADICACIÓN
4.1. EXPLICACIÓN
En tu
cuaderno escribe la siguiente información
La radicación
La radicación es la operación inversa de la
potenciación; es decir si nos dan el área de un cuadrado, extraer la raíz es
encontrar el lado de ese cuadrado; mientras que en la potenciación nos dan el
lado del cuadrado y encontramos el área.
Supongamos que nos dan un número y nos piden calcular otro, tal que, multiplicado por sí mismo un número de veces nos da el número.
Por ejemplo: calcular qué número multiplicado
por sí mismo 2 veces da 196. Ese número es 14. Porque 14 x 14 = 196
→ √196 = 14
El número que está dentro del radical se llama radicando, el grado de la raíz se llama índice y se encuentra en la V del radical, el resultado se llama raíz.
La mejor forma de encontrar las raíces de
cualquier número exacto es convertir las raíces a potencias en donde la base de
la potenciación es la raíz buscada.
Las raíces se llaman según su índice, así:
Para el índice 2 (si el índice es 2, se suele
omitir) se le llama raíz cuadrada.
Para índice 3, se llama raíz cúbica;
– índice 4, raíz cuarta; – índice 5, raíz quinta, y así
sucesivamente, es decir se nombra el número ordinal.
4.2. AFIANZAMIENTO
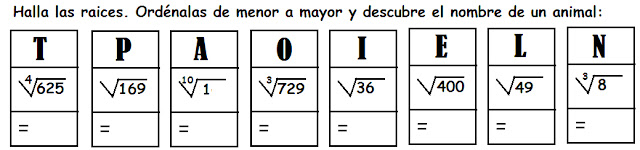
Resuelve
las siguientes raíces en tu cuaderno para ir practicando.
4.3. EJERCITACIÓN
Resuelve
las páginas 74 y 75 en tu libro de
trabajo.
ACTIVIDAD 5. LOGARITMACIÓN
5.1.
EXPLICACIÓN
Se
llaman logaritmo a la potencia que se tiene que elevar en otro número y es
llamado base del sistema, se trata en términos generales de un número positivo
sirve para obtener el mismo número. Esto es que el logaritmo es el opuesto a la
potenciación donde el logaritmo es la potencia.
Obtenemos tres términos que se llaman:
· Base del logaritmo
· Número del logaritmo
· Logaritmo
Así en una potencia:
El cinco se eleva al cuadrado y se obtiene el número 25
Aquí
en esta potenciación al pasarla a logaritmo obtenemos lo siguiente:
La
base de potencia ahora es la Base del logaritmo = 5
La potencia
ahora es el Número del logaritmo = 25
El
exponente ahora es el Logaritmo = 2 el cual se coloca en subíndice
Ahora
la forma en la que se lee el logaritmo es de la siguiente manera:
Log525 = 2
Se lee Logaritmo en base 5 de 25 = 2
5.2.
AFIANZAMIENTO
Resuelve los siguientes ejercicios para ir practicando.
5.3.
EJERCITACIÓN
B. Resuelve la página 76 en tu libro de trabajo.
ACTIVIDAD 6. MÍNIMO COMÚN MÚLTIPLO
6.1. Explicación
Para ir introduciendo el tema, mira con
atención el siguiente video.
En tu cuaderno escribe la siguiente información
El mínimo común múltiplo de
dos números a y b es el número más pequeño
que es múltiplo de a y múltiplo de b.
Para
denotar el mínimo común múltiplo de a y b escribimos m.c.m. (a, b) ó m.c.m.
(a, b).
Ejemplo:
Vamos a calcular el mínimo común múltiplo de 4
y 6. Para ello, escribimos los primeros múltiplos de 4 y de 6:
Recuerda que los múltiplos se obtienen multiplicando.
Entre los 6 primeros múltiplos de 4 y de 6, los números 12 y 24 son múltiplos de ambos (son múltiplos comunes). Tenemos que quedarnos con el mínimo.
Por tanto, el mínimo común múltiplo de
4 y 6 es 12:
En un problema, sería así:
6.2. Afianzamiento
Practica lo aprendido en los siguientes links
6.3. Ejercitación
Resuelve las páginas 81 y 82 de “Tu libro de trabajo”.
ACTIVIDAD 7. LOS POLÍGONOS (GEOMETRÍA)
7.1. Explicación
Revisa los siguientes videos
Escribe en tu cuaderno la siguiente información:
Un polígono es el área de un plano que está delimitado por líneas que tienen que ser rectas.
Si hacemos caso a la
etimología de la palabra, polígono proviene de los términos griegos «poli»
y «gono». «Poli» podría traducirse como «muchos» y «gono»
como «ángulo». Atendiendo a esto podríamos decir que un polígono es
literalmente aquello que tiene muchos ángulos.
Para considerar polígono a
una figura esta debe cumplir que sus líneas siempre deben ser rectas y que no
puede estar abierto. En la siguiente imagen puedes ver varios ejemplos de
polígonos y otros que no lo son:
Luego lee la información que se
encuentra en la página 132 de “Tu libro de trabajo” con el título “Debes
aprender”.
Dibuja enseguida dibuja los siguientes polígonos
regulares e irregulares.
7.2. Afianzamiento
Realiza la siguiente actividad para practicar. No debes escribir nada en el cuaderno.
7.3. Ejercitación
Resuelve la página 132 de “Tu libro de trabajo”.
ACTIVIDAD
8. MÁXIMO COMÚN DIVISOR
8.1. Explicación
Para ir introduciendo el tema, mira con atención el siguiente video:
En tu cuaderno escribe la siguiente información.
Los divisores de un número
Los divisores de un número natural son los números naturales que lo pueden dividir, resultando de cociente otro número natural y de resto 0.
Ser divisor es lo contrario
a ser múltiplo. Si 9 es múltiplo de 3, entonces 3 es divisor de 9.
Los divisores de un
número natural le pueden dividir, su división es exacta.
Cada número tiene una
cantidad concreta de divisores. El número 1 tiene sólo un divisor, él mismo.
Solamente el 0 tiene
infinito número de divisores, ya que todos los números son divisores de 0.
Por ejemplo:
D12= {1,2,3,4,6,12}
D30=
{1,2,3,5,6,10,15,30}
D8= {1,2,4,8}
En un
problema sería lo siguiente:
En el almacén, tengo cajas de todos los tamaños ¿de qué forma puedo empaquetar 12 latas de refresco en cajas iguales sin que me sobre? Puedo agrupar las 12 latas de 6 formas diferentes.
Para empaquetar las 12
latas, podemos utilizar cajas de 1, 2, 3, 4, 5, 6 y 12 unidades.
8.2. Afianzamiento
Practica lo aprendido en los siguientes links: PRÁCTICA 1 y PRÁCTICA 2
8.3. Ejercitación
Resuelve las páginas 70 y 71 de tu libro de trabajo.
ACTIVIDAD
9. CLASIFICACIÓN DE LOS POLÍGONOS (GEOMETRÍA)
9.1. Explicación
Revisa el siguiente video:
Escribe en tu cuaderno la siguiente información:
Clasificación de polígonos
Podemos clasificar los polígonos de tres formas diferentes:
- Clasificación de polígonos según sus lados:
- Triángulo: 3 lados
- Cuadrilátero: 4 lados
- Pentágono: 5 lados
- Hexágono: 6 lados
- Heptágono: 7 lados
- Octógono: 8 lados
- Eneágono: 9 lados
- Decágono: 10 lados
- Endecágono: 11 lados
- Dodecágono: 12 lados
- Clasificación de polígonos según sus ángulos:
- Polígonos cóncavos: es cuando el polígono tiene un ángulo que mide más de
180º.
- Polígonos convexos: es cuando todos los ángulos del polígono miden menos de
180º.
- Clasificación de polígonos según sus lados y sus
ángulos:
- Polígonos regulares: es cuando un polígono tiene todos sus lados y ángulos iguales.
- Polígonos irregulares: es cuando en un polígono hay uno o más lados y/o ángulos que no
son iguales.
9.2. AfianzamientoRealiza las siguientes actividades para practicar. No debes escribir nada en el cuaderno.
https://www.mundoprimaria.com/juegos-educativos/juegos-matematicas/juego-identificacion-figuras
https://www.mundoprimaria.com/juegos-educativos/juegos-matematicas/juego-vertices-y-angulos
https://www.mundoprimaria.com/juegos-educativos/juegos-matematicas/juego-poligonos-regulares
9.3. Ejercitación
Resuelve las páginas 133 y 134 de tu libro de trabajo.
ACTIVIDAD
10. NÚMEROS PRIMOS Y COMPUESTOS
En tu cuaderno escribe la siguiente información:
NÚMEROS PRIMOS Y COMPUESTOS
Los números
primos son aquellos que solo, muy importante, solo son divisibles (al
dividirse entre otro da un número entero) entre ellos mismos y el 1.
Por ejemplo: el 7 es un
número primo porque solo es divisible por 7 y por 1. Otro ejemplo, el 13 es un
número primo porque solo lo podemos dividir entre 1 y 13. Además, se puede
escribir como la multiplicación de 1×13, pero no como otra multiplicación de
números naturales.
Los números compuestos son aquellos que son divisibles por ellos mismos, por la unidad y también por otros números. Recuerda, el número 1 no se considera ni compuesto ni primo por convenio.
El 25 es un número
compuesto. Entonces es divisible por 1, por 25 y por 5. Es decir, 25/25= 1,
25/1= 25 y 25/5=5.
El 14 es un número
compuesto y no es primo. Es divisible por 1, por 2, por 7 y por 14. Lo
comprobamos: 14/1 = 14, 14/2 = 7, 14/7 = 2 y 14/14 = 1.
Estos son los números primos hasta el 1.000
ACTIVIDAD
11. POLÍGONOS CÓNCAVOS Y CONVEXOS (GEOMETRÍA)
11.1. Explicación: Revisa el siguiente video:
Escribe en tu cuaderno la siguiente información que encuentras en la página 135 de tu libro de trabajo en la parte “DEBES APRENDER”.
11.2. Afianzamiento: Realiza las siguientes actividades.
A. Resuelve en el cuaderno:
B. Explora las páginas. No debes escribir nada en el cuaderno:
11.3. Ejercitación
















No hay comentarios.:
Publicar un comentario